Enigme n° 32 : Origine du rayon des atomes

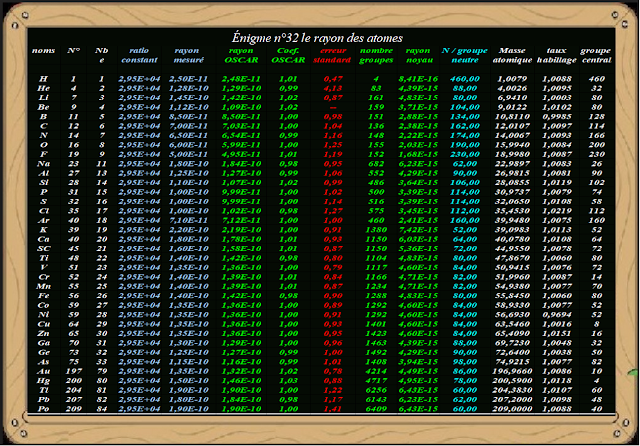
- Sceptique : on trouve une grande diversité de rayons des atomes et des divergences entre le calcul standard et la mesure. Il y a par exemple l'hélium 4 où le MS calcule un rayon de (31 pm) alors que la mesure indique 128 pm (picomètres) → pm = 10⁻¹² m. Que dit le modèle OSCAR ?

- Le tableau suivant montre qu'avec la règle de calcul unique d'Oscar, on obtient une bien meilleure cohérence avec les mesures que la méthode du MS. Les atomes ne sont pas conformés en grappes (proton-neutrons) comme le suppose le MS mais construit en couches sphériques concentriques représentant la partie neutre + des positrons célibataires donnant la charge du noyau. La règle est simple car elle utilise la loi universelle : ℳ.ℒ = Cte  qui permet de fixer la base qu'est le rayon du proton,  rₚ . Plus la masse d'un groupe est grande, plus le rayon est petit ! Ensuite on pose :

Rₓ = rₓ 𝛼² 𝜋 / 2  

pour trouver le rayon de l'atome x avec rₓ = 𝜆ₑ / 2 𝜋 ng, soit le rayon de Compton de l'électron / nombre par groupe. Le nombre par groupes est forcément pair car il est neutre. Par exemple le proton possède 4 groupes neutres de 460 unités nues + 1 positron célibataire. L'hélium  possède 83 groupes neutres de 88 unités nues dont un (au centre) réduit à 32 unités + 2 positrons célibataires.  Par définition chaque nombre par groupe doit être pair pour répondre au critère de neutralité. Dans certaines conditions, des paires de Cooper se forment dans le cadre des unités célibataires non incluses dans les groupes neutres complets.  Il suffit de parcourir le tableau pour s'apercevoir que cette même règle de calcul est toujours cohérente avec les mesures, ce qui n'est pas le cas avec le calcul du MS.

- Sceptique : pourquoi le noyau d'hélium est un boson de spin 0 alors que le neutron a un spin 1/2 ?

- On verra cela dans le prochain billet mais il est clair que la paire neutre célibataire du neutron ne peut pas former une paire de Cooper.  

- Sceptique : Que sont les autres bosons de spin zéro ?

- En plus des paires de Cooper et de certains noyaux d'atomes, il y a le boson de Higgs dont on a vu qu'il matérialise l'extraction d'un dipôle subquantique dans lequel les deux spins opposés s'annulent. Par ailleurs il existe des bosons de spin entier ( photons, W, Z). Par exemple le boson W matérialise l'extraction subquantique d'une paire de pôles de spins de même signe (1/2 + 1/2 = 1).