Enigme 63 : le point zéro

-
Voir : sommaire des énigmes , les cinq clés de la physique fondamentale  et l'éclaté du modèle Oscar.





- Sceptique : quelle est la taille du point zéro d'un  BEC-fils et comment peut-il émettre et recevoir 𝜉⁹ pôles de ℬodys toutes les 1.288×10⁻²¹ secondes (te) ? 

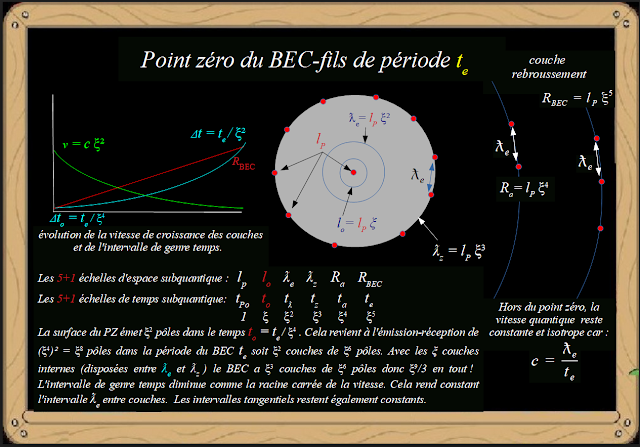
- Le tableau montre que l'on retrouve encore ici les 5+1 échelles liées à la mitose . Le rayon du "point zéro commun" vaut : ƛz = 5,96 cm = 𝜉 ƛe = 𝜉² lo. Les 5+1 échelles spatiales subquantiques commencent avec la longueur de Planck lp et terminent avec le rayon du BEC. L'échelle de temps est rapportée à cette échelle subquantique spatiale. La surface du PZ ne peut émettre (ou recevoir) que 𝜉² pôles en même temps. Via l'intervalle temps subquantique tpo. est 𝜉⁴ fois moindre que la période du BEC te. Le PZ peut donc émettre 𝜉² × 𝜉⁴  = 𝜉⁸ pôles qui multipliés par 𝜉 pôles contenus dans le PZ permettent de remplir le BEC de 𝜉⁹/3 ℬodys . Il faut leur soustraire les  𝜉⁶ ℬodys devenus des paires électron-positrons fusionnées en protons. Cependant cette soustraction est totalement négligeable sur le nombre 𝜉⁹/3 .
 
- Sceptique : pourquoi cette division par 3 ?
 
- C'est le facteur d'intégration d'une sphère solide constituée d'une infinité de cercles concentriques. La surface maximale est : S = 4 𝜋 r² et donc V = 4 𝜋 r² × r/3. Les facteurs d'intégrations peuvent être négligés pour simplifier. 

- Sceptique : comment nourrir des couches pour maintenir les intervalles constants dont la surface est en croissance d'un facteur (𝜉²)²  = 𝜉⁴ ?
 
- La surface des couches augmente en r² alors que vitesse varie en 1/r². C'est le ralentissement qui compense l'augmentation de surface.
 
- Sceptique : la constance des intervalles est-elle respectée à l'intérieur du point zéro commun ? 
 
- Non car il y a forcément juxtaposition pour assurer la synchronisation . Par exemple on note que le volume du PZ est calibrer pour contenir (𝜉³)³ = 𝜉⁹ ℬodys ayant la taille de Planck.
 
- Sceptique : donc la longueur de Planck est la taille inférieure du niveau subquantique. Mais pourquoi le temps de Planck subquantique est  𝜉³ fois plus petit que le temps de Planck connu ?
 
-  Tout simplement à cause du fait que la vitesse subquantique est 𝜉³ fois plus grande que c. Il est du genre intervalle car ne matérialisant pas une   période d'oscillation.         
 
 

Commentaires

  1. Dominique MAREAU24 octobre 2019 à 08:38

    La dualité quantique-subquantique fait que la période (sub) du BEC "te" est égale à celle (qua) de l'intervalle élémentaire. Le ratio entre les deux niveaux est donc xi^3. Il existe donc un temps de Planck (sub) qui est xi^3 fois plus petit.

    RépondreSupprimer

Enregistrer un commentaire

Posts les plus consultés de ce blog

Le néant se précise en cassant le mythe du spin

-
Beaucoup de physiciens se demandent si l'électron tourne vraiment. Bien sûr Pauli et Dirac arrivent à la conclusion que cela ressemble à une rotation... - Le premier élément allant dans ce sens est la dimension de la constante de Planck,  h . Cette dimension [M L² / T] correspond effectivement à un moment cinétique ou quelque chose se trouvant en orbite. Cela se traduit par une impulsion p [M L / T] s'exerçant sur le rayon r   ou [L] d'un cercle. - Le second élément allant dans ce sens, est l'ancienne conception (modèle de Bohr) d'un électron orbitant autour d'un proton, un peu comme une planète autour d'une étoile... Là encore, on attribut un rôle de spin à la constante de Planck, h . Mais depuis, l'eau a coulé sous les ponts. - Déjà le second élément (modèle planétaire) a laissé place à une vue plus quantique où l'électron orbital est en fait sous forme d'une onde sphérique dont les coordonnées se traitent en terme de probabilité. ...
Lire la suite

L'atome Schrödinger-Oscar

-
Image
Le modèle standard a nettement progressé sur la représentation de l'atome depuis Thomson en 1899. En figure 1, on note la progression de la connaissance de l'atome. La naïve représentation de l'atome de Thomson, ressemble étrangement à celle que le modèle standard se fait encore actuellement, du noyau ( en grappe ). Ensuite la représentation de l'atome de Rutherford (en 1911), un peu plus réaliste, était inspirée du système planétaire gravitant autour du soleil. Le modèle de Bohr en (1913) avait inclus l'idée d'une quantification qui donnait des orbites stables aux électrons. Mais un certain nombre d'expériences indiquaient un comportement étrange du monde subatomique qui ne collaient pas avec le dernier modèle en cours. En 1925, Schrödinger propose un modèle d'essence mathématique qui se révélera en accord avec l'expérimentation. Figures 1 : évolution des modèles d'atomes    1. Le modèle de Schrödinger  : il s'e...
Lire la suite

La double dualité de cette bulle univers

-
Image
Dans l'article précédent, nous avons vu les deux constantes aléatoires : le facteur d'annihilation (2D) primordiale  a²   et le facteur de mitose  ξ² . Nous avons vu également que les oscillateur-tachyons synchronisés possédaient une constante :   M × L qui reste en vigueur dans la paire électron-positron.  A cette échelle, il n'existe pas de masse M ou de longueur L séparées. L'une est toujours le reflet de l'autre. Dans l'oscillateur dipolaire, quand M tend vers zéro, la réponse (déphasée) est L qui tend vers l'infini. Comme pour une corde de guitare, plus L est grand et plus M est grand, plus la note est grave. Une note grave revient à une basse fréquence et donc un temps de cycle T long ou grand. On a T = f(ML) .  On montre que le temps élémentaire T – commun pour l'électron, le BEC ou le tachyon – dépend de  ML.  Ainsi chaque bulle univers est caractérisée par cette double dualité : La dualité de  ratios  a²   et...
Lire la suite